Quick Sort

Entenda e aprenda a implementar o algoritmo de ordenação Quick sort em Java

O algoritmo Quick sort possui alta performance para ordenar uma lista com muitos elementos (O(n * log n)).

Devido a isso, ele é um pouco mais complexo de se implementar dos que os algoritmos estudados anteriormente como os de ordenação por seleção ou inserção.

Isto implicará em um maior esforço e revisar o código múltiplas vezes até que ele possa entendido.

Assim como o Merge sort, o Quick sort também utiliza o princípio de dividir para conquistar para ordenar a lista.

Sua estratégia consiste em selecionar um elemento como o pivô, normalmente o último elemento da lista.

Uma vez selecionado o pivô, um método chamado partição será o responsável por colocar o pivô em sua posição correta, mantendo os números menores do que ele a esquerda, e os maiores a direita.

Com base na posição final do pivô, a lista é divida em duas (esquerda e direita ao pivô), e o mesmo método de partição é chamado para cada um das listas.

Este processo ocorre até que as listas contenham apenas um elemento, que é quando as chamadas recursivas terminam.

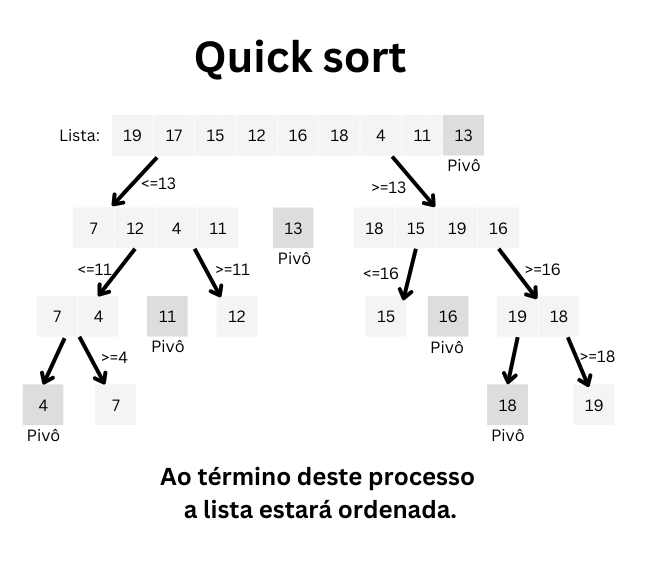
Ao término de todo o processo a lista estará ordenada.

Veja na imagem a seguir uma simulação de como ele ordena uma lista:

Vamos agora ver a implementação deste algoritmo em Java, e na sequência estudaremos em detalhes o código:

public void ordenarQuickSort(int[] listaOrdenar, int inicio, int fim) {
    if (inicio < fim) {
        int indiceParticao = particao(listaOrdenar, inicio, fim);

        // ordena recursivamento os elementos contido antes e depois da partição
        ordenarQuickSort(listaOrdenar, inicio, indiceParticao - 1);
        ordenarQuickSort(listaOrdenar, indiceParticao + 1, fim);
    }
}

private int particao(int[] listaOrdenar, int inicio, int fim) {
    int pivo = listaOrdenar[fim];
    int i = (inicio - 1); // índice do menor elemento
    for (int j = inicio; j < fim; j++) {
        if (listaOrdenar[j] <= pivo) {
            i++;
            if (i == j) {
                continue;
            }
            int temp = listaOrdenar[i];
            listaOrdenar[i] = listaOrdenar[j];
            listaOrdenar[j] = temp;
        }
    }

    int temp = listaOrdenar[i + 1];
    listaOrdenar[i + 1] = listaOrdenar[fim];
    listaOrdenar[fim] = temp;

    return i + 1;
}

O método recebe somente três parâmetros (int[] listaOrdenar, int inicio, int fim), que são a lista a ser ordenada, o índice da posição utilizada como o início da lista, e o índice da posição utilizada como o fim da lista.

Pelo fato dele ordenar os elementos na própria lista de entrada ao final da execução, ele não retorna nada uma vez que ao final de sua execução o parâmetro de entrada estará ordenado.

O Quick sort não cria listas auxiliares, ele usa somente a de entrada para ordenar os dados, e pelo fato dele fazer divisões para as chamadas recursivas, sempre passamos os índices de início e fim para demarcar os elementos da listas para uma determinada chamada.

Ele possui também dois métodos, o principal ordenarQuickSort, que basicamente coordenada as chamadas recursivas e parada das mesmas, e o segundo chamado particao, que é o responsável por fazer as alterações na lista.

Vamos iniciar o estudo pelo primeiro método, ordenarQuickSort, que inicia com o critério de parada das chamadas recursivas, comparando os valores dos índices inicio e fim, pois caso inicio seja menor do que fim, isto significa que não existem elementos neste bloco da lista.

Feito isso, ele chama o método particao, este que sejá estudado logo em seguida, que basicamente retorna o índice do elemento pivô na lista.

Com o valor deste índice, o método principal faz duas chamadas recursivas a ele mesmo, onde dividimos a lista em duas com base nos elementos que estão a esquerda e direita do pivô.

Veja no código a seguir como estas chamadas são feitas com base no índice da partição para definir os valores de inicio e fim:

int indiceParticao = particao(listaOrdenar, inicio, fim);

// ordena recursivamento os elementos contido antes e depois da partição
ordenarQuickSort(listaOrdenar, inicio, indiceParticao - 1);
ordenarQuickSort(listaOrdenar, indiceParticao + 1, fim);

Agora vamos ver o método particao, que recebe os mesmo parâmetros do método anterior.

Ele inicia obtendo o elemento pivô, que no caso é o último elemento da lista neste implementação:

int pivo = listaOrdenar[fim];

Depois definimos i, que conterá o índice do menor elemento na lista, utilizado para as trocas. Ele é inicializado com o valor contido em inicio - 1, pois a seguir ele será incrementado no código e conterá o índice do primeiro elemento da lista, conforme código a seguir:

int i = (inicio - 1); // índice do menor elemento

Agora chegou a hora de implementar um laço do tipo for responsável por iterar em todos os elementos da lista.

No laço for, verificamos se o elemento corrente é menor ou igual ao pivô, e caso seja, incrementamos o valor de i, e fazemos a troca entre os valores da lista contidos nos índices i e j.

Adicionamos uma pequena verificação antes da troca para garantir que os valores de i e j sejam diferentes, pois caso eles sejam iguais não precisamos fazer a troca por estarmos falando do mesmo número. Veja a seguir o bloco de código referente a esta parte do código:

for (int j = inicio; j < fim; j++) {
    if (listaOrdenar[j] <= pivo) {
        i++;
        if (i == j) {
            continue;
        }
        int temp = listaOrdenar[i];
        listaOrdenar[i] = listaOrdenar[j];
        listaOrdenar[j] = temp;
    }
}

Ao término do laço for, fazemos mais uma permutação de elementos na lista, mas desta vez entre o valor contido em i + 1 e o pivô (listaOrdenar[fim]), que será colocado em sua posição correta, conforme o código a seguir:

int temp = listaOrdenar[i + 1];
listaOrdenar[i + 1] = listaOrdenar[fim];
listaOrdenar[fim] = temp;

Para finalizar, este método retorna o índice do pivô na lista, que após a último permutação, ele passou a ser i + 1, conforme o código a seguir:

return i + 1;

Ao término deste processo, a lista (listaOrdenar) estará ordenada e o algoritmo terminará.

Conforme mencionado no início, o algoritmo possui múltiplas etapas e será necessário a revisão do código para seu completo entendimento.

Quanto a sua performance, ele sendo de ordem O(n * log n) significa que ele sempre passará por todos os elementos (n), mais um processamento extra de log n, pois ele precisa fazer alguns ajustes para concatenar a lista, e mesmo com todo este processamento ele ainda assim possui boa performance pois o incremento de log n tem um crescimento baixo e consegue processar múltiplos elementos sem um aumento expressivo no número de operações necessárias para concluir a ordenação.

Com isso, terminamos o estudo do algoritmo Quick sort.